Rainbow Tables are a type of password hash tables that help simplify the process of cryptanalysis by applying a set of time-memory trade-offs to make the process be more efficient. They were proposed by Philippe Oechslin as a way to improve on the pre-existing concept of Time-Memory Trade-Offs that can be leveraged to run password attacks, reducing computation time, calculations and false alarms, compared to the original method.
To understand what they are, let’s first elaborate on a few concepts:
A hash function is a mathematical function that receives data on its input, and maps it to values of the same length on the output. There are many hash algorithms, with MD5, SHA-1, SHA-256, SHA-384 and SHA-512 being among the most used in cryptography. Hash functions are a kind of one-way cipher function, because they allow enciphering plain text into cipher text, but they cannot decipher the plaintext
version of a given cipher text.
For example,
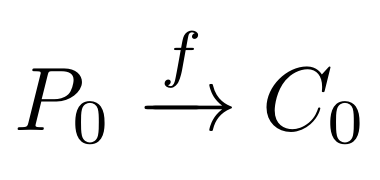
Where f is the hash function.
Cryptanalysis is explained by Martin Hellman’s A Cryptanalytic Time-Memory Trade-Off paper as the problem of going through a set of precomputed password hashes to find the plaintext version of a password that was hashed, prior to being stored on a system.
Original Method
Hellman’s original method is based on making a compromise between the amount of memory needed to crack a password, and the amount of operations needed to perform the attack. It focuses on leveraging T operations (time) and M words of memory to search through N possible keys; which have to be computed previously.
The process of precomputing these solutions consists of specifying a long-enough word list (preferably with many word combinations) as a starting point on the left column of the table.
For each row in the table, you take the original block (whether or not it’s plaintext), apply an encipherment function to it (such as a hashing algorithm); and then you apply a reduction function to the resulting cipher text.
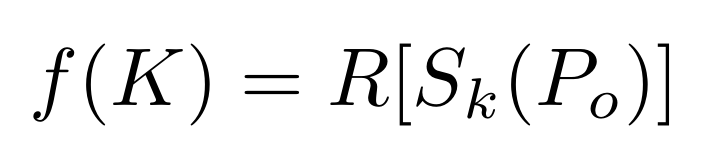
Where R is a reduction function. – i.e. If the cipher text is 64-bits long, a reduction function could drop the last 8 bits to produce a 56-bit result.
After you’ve applied the cipher function(f) to the starting point (the plaintext), you apply f to the result of the first operation; then continue iterating for a total of t times. Thus, the chain will be of length t; and then you move on to the next chain, as illustrated by the following graph:
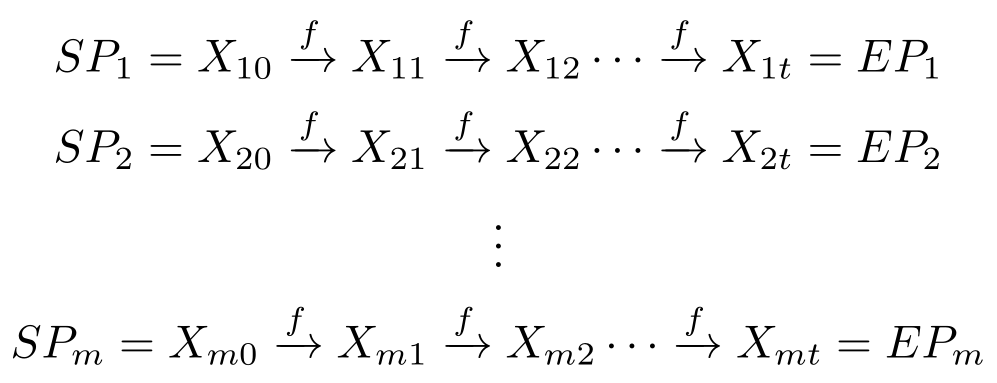
Once a chain has reached length t, we only store the value of the Starting Point ![]() and the End Point
and the End Point ![]() in the table.
in the table.
Due to the iterative nature of chains, there is a chance that 2 or more chains merge, because a result of a computation (either ![]() or an end-point
or an end-point ![]() ) might have 2 or more inverse images, generating a false alarm.
) might have 2 or more inverse images, generating a false alarm.
This is supposing that we’re using the same reduction function (R) for all iterations of f, on all chains. However, since there are tons of possible reduction functions, and to improve the probability of success, you need to generate many tables (actually a total of t tables), each with a different choice of R.
All entries on the table are sorted by End Point; so when running an attack, you would search for the cipher text on the End Points column. Once you’re in the correct range of rows, you take the value at the Starting Point ![]() column and compute
column and compute ![]() ) a total of N times to compute only that chain. If the ciphertext is found on the chain, you look at the previous iteration of the function to see if it is the key (i.e. check if it is the password you’re searching for). In case the cipher text is not found in the chain, you would either move to the next row and compute that chain, or move to another table to search there. For each line on a table, you will indeed need to compute the new chain. However, if it isn’t the key, then you go to the previous iteration, and again, and again, until you find the correct key.
) a total of N times to compute only that chain. If the ciphertext is found on the chain, you look at the previous iteration of the function to see if it is the key (i.e. check if it is the password you’re searching for). In case the cipher text is not found in the chain, you would either move to the next row and compute that chain, or move to another table to search there. For each line on a table, you will indeed need to compute the new chain. However, if it isn’t the key, then you go to the previous iteration, and again, and again, until you find the correct key.
Rainbow Tables
As explained previously, Rainbow Tables were proposed by Philippe Oechslin as an improvement to both the original method by Hellman and some others like Distinquished Points, as he references in his research paper. Instead of generating multiple tables, each with a different reduction function (![]() ), these implement a single table of dimensions mt*t, using a different reduction function for each iteration of the chain.
), these implement a single table of dimensions mt*t, using a different reduction function for each iteration of the chain.
Knowing that each function is given by ![]() , therefore the table would be constructed
, therefore the table would be constructed
something like this:
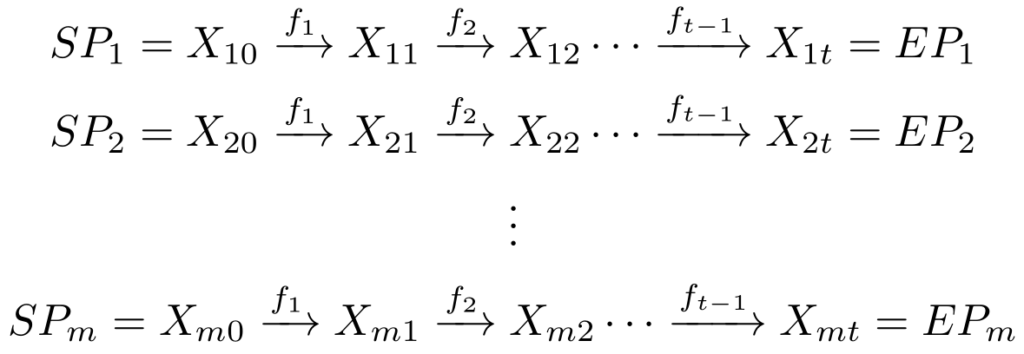
The advantage of this method over the original is that, first, we get a lot less number of table look-ups, with the added benefit of getting a lot less false alarms, which means that we spend a lot less time doing cryptanalysis and also that we get an answer a lot quicker than with the orignal method.
There’s also the added benefit that using distinguished points, each chain would have a variable length, which leads to an increased overhead because, if 2 or more chains merge and cause a false alarm, we have to compute the entire length of each of the chains, so that we can detect the false alarm. Meanwhile, the constant length of rainbow table chains means we only need to compute a fraction of the chain, because we know exactly the position of the chain where we should locate the merging key, reducing the time cost of a false alarm.
According to Dr. Oechslin’s experimental results, by using 5 rainbow tables the number of hash computations was reduced by a factor of 12 compared to applying distinguished points to the original method, by analyzing all tables as well.
Mitigation Strategies
Over time, Rainbow Table attacks have become less popular, mainly because of the introduction of salts in encryption. A salt is a technique where, after computing the hash of the original password, you append a random number to the cipher text.
For example, with the password: p8c6uMTMVGgKjLoBG4p04xtTk, the generated SHA-512 hash would be . However, if we were to append the salt 13db61b6c98387, the plaintext would look like this:
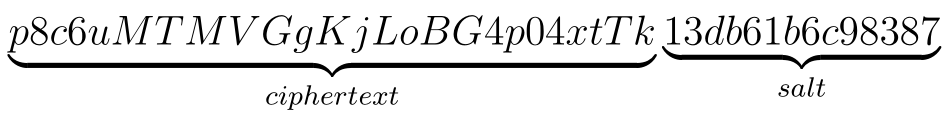
Which would result in the following SHA-512 hash:
ac6b3367618ffa34bbedc0416aea644c598439ce3a696769a9ce5e4708ed02d95d2ae9f702f2a3e2d6d967ae9b0f2ef3cfba9e2422e5c8cbb764b56021e51e5e
Even though rainbow tables aren’t as popular as they were before, knowing about how they work is still useful, because, if you’re doing a pentest, you never know when you might run into an old server that uses Microsoft LAN Manager, which is in fact vulnerable to Rainbow Tables.
Fortunately, there are several tools that allow you to crack passwords using rainbow tables. For example, Kali Linux comes with OphCrack and RainbowCrack.
