DNSENUM Tutorial – DNS Information Gathering Tool: We are back with “Know your Backtrack” i.e. KYB Tutorial 2. Today we will learn about another information gathering tool: DNSENUM. The purpose of Dnsenum is to gather as much information as possible about a domain. Basically its an perl script and it performs the following operations:
1) Gets the host’s address (A record).
2) Gets the namservers (threaded).
3) Gets the MX record (threaded).
4) Performs axfr queries on nameservers and gest BIND versions (threaded).
5) Gets extra names and subdomains via Google scraping (Google query = “allinurl: -www site:domain”).
6) Brute force subdomains from file, can also perform recursion on subdomain that have NS records (all threaded).
7) Calculates C class domain network ranges and perform whois queries on them (threaded).
8) Performs reverse lookups on net ranges ( C class or/and whois net ranges) (threaded).
9) Writes to domain_ips.txt file ip-blocks.

DNSENUM Tutorial
So let’s start our DNSENUM Tutorial with a basic example: suppose we want to gather DNS information of a domain, for example hackingloops.com. This is how we will proceed:
1. To start DNSENUM, first start the backtrack, then follow below the path:
Backtrack >> Information Gathering >> Network Analysis >> DNS Analysis >> dnsenum
Now the terminal will open with the DNSENUM script loaded with the list of all sub commands that we can use with DNSENUM.
2. To gather DNS information from hackingloops, type the following command in the terminal :
./dnsenum.pl hackingloops.com
Below are screenshots:
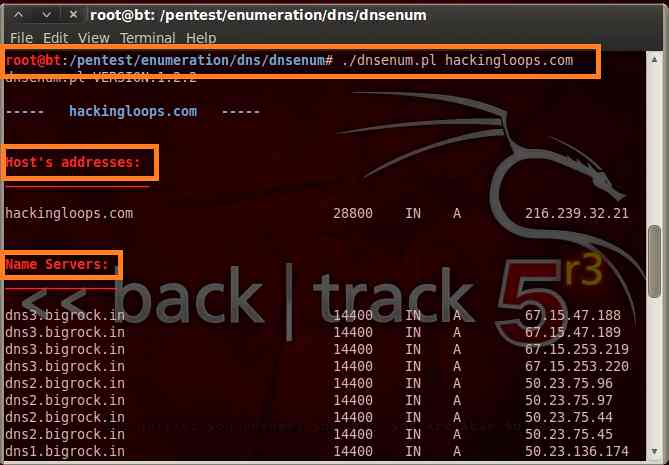
How to use DNSENUM Tool
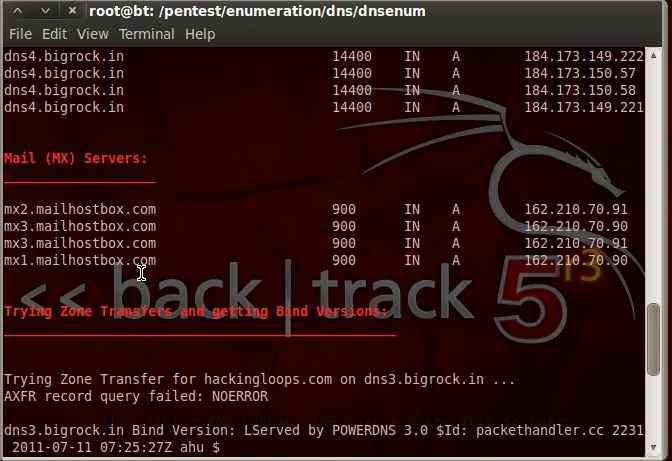
using DNSENUM part 2
So we can see by just giving a simple command we have name servers, mail servers, host address and many more.. The results vary from website to website and scope enhances when there are sub domains in the target website.
We can also use DNSENUM to scrap the sub domains of a website from Google. For doing this we need to type below command :
./dnsenum.pl -p 1 -s 1 example.com
Scrapping will not work on those websites which do not have sub domains and for websites which have restricted wild card scrapping.
That’s all for today. You can practice multiple combinations and sub commands mentioned below to extract juicy information regarding DNS’s for any domain.
COMMANDS ENCYCLOPEDIA :